上一篇已針對Direct topology, Indirect topology, Diameter, Bisection width, Number of edges per switch與 是否Constant edge length

做出定義與介紹

本篇延續上篇，繼續運用上述方法來分析相關的網路拓璞(Topology)

首先來複習一下 2-D Mesh

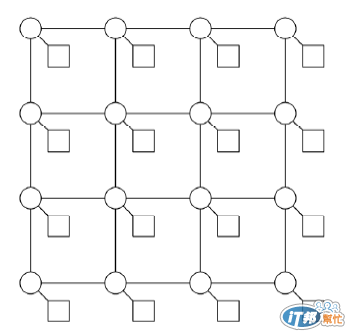
圓圈代表Switch, 方形代表 Processor，這是一個4x4共16個點的示意圖，上篇討論過

今天來討論推廣到n個點(即 根號n x 根號n )的情形 (這裡的n一律都指處理器Processor的數量)

1. Switch : Processor 是 1:1 也就是數量一樣多，所以這是一張 Direct Topology

2. Diameter: Θ(n^1/2) 根號 n <-- 因為從最右上到最左下，每一步往右或往下走都有兩種可能，所以推廣到n個點就會需要走複雜度 n^1/2 (n的二分之一次方)個點！

3. Bisection width: Θ(n1/2) 根號 n <-- 由 4x4 的圖可見 Bisection witdh 是 16^1/2 (根號16) = 4 符合！

4. Number of edges per node: 4 如圖可看出，推廣到n個處理器，就會有n個switch，中間的每一個switch都會接四條線到其他四個人

5. Constant edge length? YES ! 一個switch連到下個switch之間，每一條"邊"都是等長的

再來討論一下二元樹的Topology的情形：

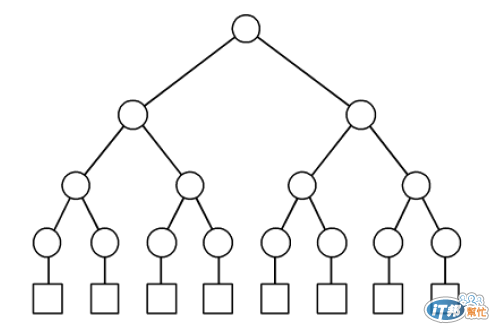
一樣來討論推廣到n個正方形點的情形 (這裡的n一律都指處理器Processor的數量)

並且假設二元樹的深度為d

則這顆二元樹共有 2^d 個處理器，即n= 2^d，且switch的數量為 2n -1 最下面那層的兩倍扣掉最上面那顆root只有一個的狀況

驗證：例如上圖的二元樹示意圖深度 d = 3 從最上面的root總共往下長了三層，則最下層有2^3 = 8的圓點！即共有8個方點

整棵樹全部共有2x8-1 = 15 個圓點。

分析：

1. Switch : Processor > 1:1 也就是switch數量比較多，所以這是 Indirect Topology

2. Diameter: 2*log(n)<-- 從左邊最下層要先走到最上層root，再往下走到最下層的距離為最長，

從最下面走一趟到最上面共經過 log(n) 個點，所以上來一趟下去一趟，共兩趟所以要乘以二 -> 2*log(n)

p.s. 這裡用的 log 都是以2為底。

3. Bisection width: 1 要切斷成兩張圖太容易了，隨便選一條邊切下去，就會斷成兩半，成了兩棵比較小的tree

4. Number of edges per node: 3 如圖可看出，推廣到n個處理器的情形下，中間的每一個switch都會上方接一條，下方接兩條，共三條線！

5. Constant edge length? NO! 隨著樹越長越"高"，最下層就會越龐大，連結的網路線的長度就會越長！所以長度就不是Constant的

二元樹的Bisection width實在是太糟糕了，很脆弱

所以又有了這種 Hypertree Network

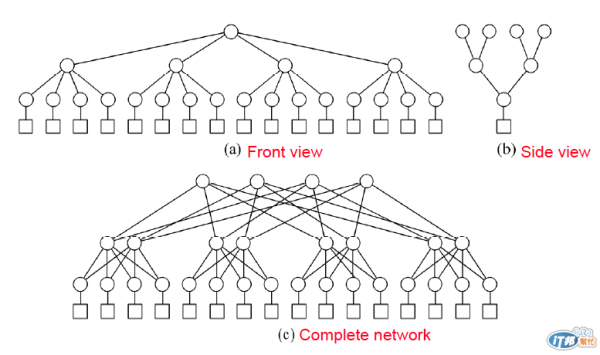
這個tree跟二元樹有點像，只是每一個節點要往下接 4 個點！

跟二元樹不同的點在於，每一個點除了往下生4個child以外，還要往上接兩個！

所以root那層最基本就有了四個點！

分析：

1. Switch : Processor > 1:1 也就是switch數量比較多，所以這是 Indirect Topology

2. Diameter: 2d = 2*log(n) 從左邊最下層要先走到最上層root，再往下走到最下層的距離為最長，

從最下面走一趟到最上面共經過 log(n) 個點，所以上來一趟下去一趟，共兩趟所以要乘以二 -> 2*log(n)

p.s. 這裡用的 log 都是以4為底。

3. Bisection width: n/2

4. Number of edges per node: 6 每個節點上方接 2 條，下方接 4 條，共6條線！

5. Constant edge length? NO! 隨著樹越長越"高"，最下層就會越龐大，連結的網路線的長度就會越長！所以長度就不是Constant的

(明日待續)